1.12 – Practice Problem 2¶
Question¶
In wastewater treatment, an important step in the process is sedimentation. Sedimentation is the process of allowing particulate matter in a fluid to settle to the bottom of a tank. In the sedimentation step, a coagulant can be used to coagulate bacteria and fine particles to allow the sedimentation to occur faster. The most common molecular species used for coagulation is alum, \(Al_2 (SO_4)_3 \cdot 14H_2 O\).
You are a chemical engineer working in a waste water treatment plant. You are asked to make a material balance on the sedimentation process. Waste water flows into a sedimentation tank at 200 kg/s. The waste water contains 0.01 wt% of bacteria, 2 wt% particulate matter, and the balance pure water. Pure alum is added to the sedimentation tank in a separate stream. Alum allows 80% of the bacteria and 100 % of the particulate matter to settle. Just enough alum is added for this ratio of settlement. The sludge at the bottom of the tank exits the tank with 20 wt% of water and 40 wt% of particulate matter. The semi-treated water exits the tank in a separate stream.
- Draw and label a block flow diagram (BFD).
- Perform a degree of freedom analysis.
- Fully balance the remainder of the block flow diagram.
Answer¶
a) Draw and label a block flow diagram (BFD)¶
First, let’s draw the basic layout of the BFD:
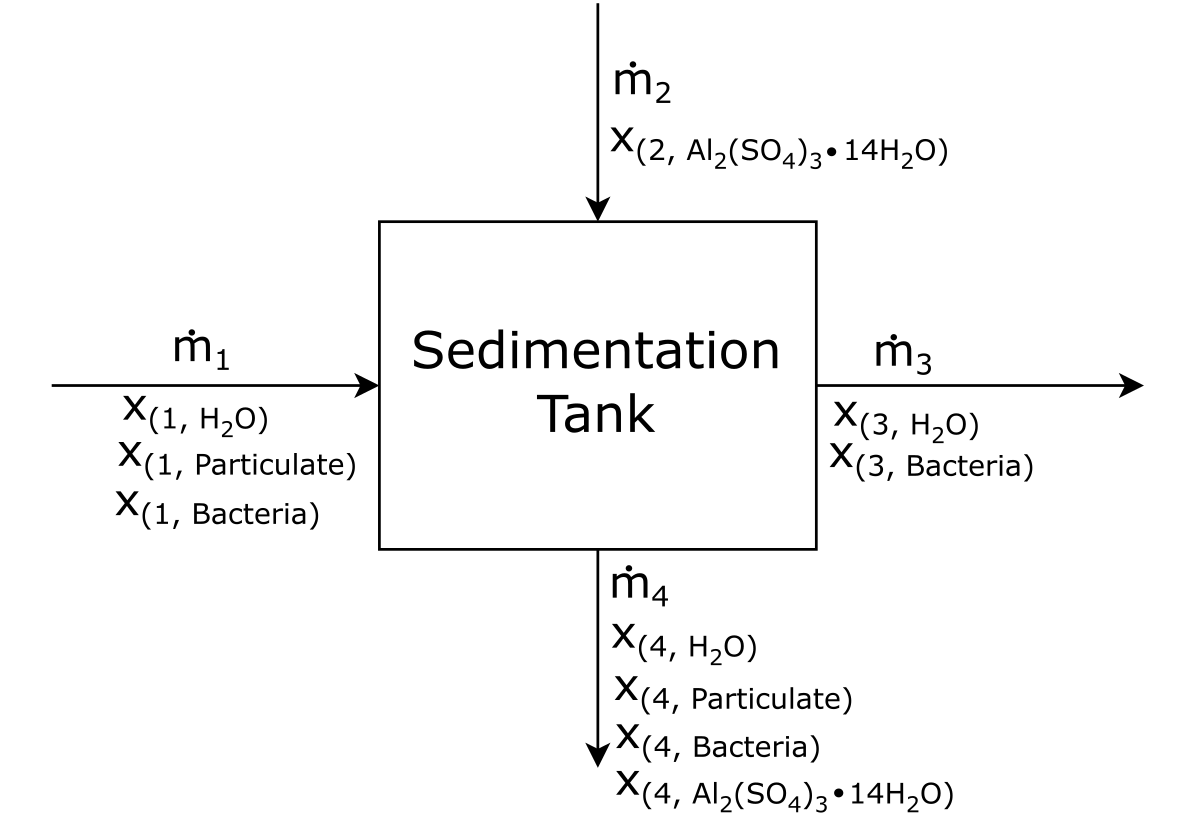
Attribution: Said Zaid-Alkailani & UBC [CC BY 4.0 de (https://creativecommons.org/licenses/by/4.0/)]
Using the information given, let’s fill out as much of the BFD as we can.
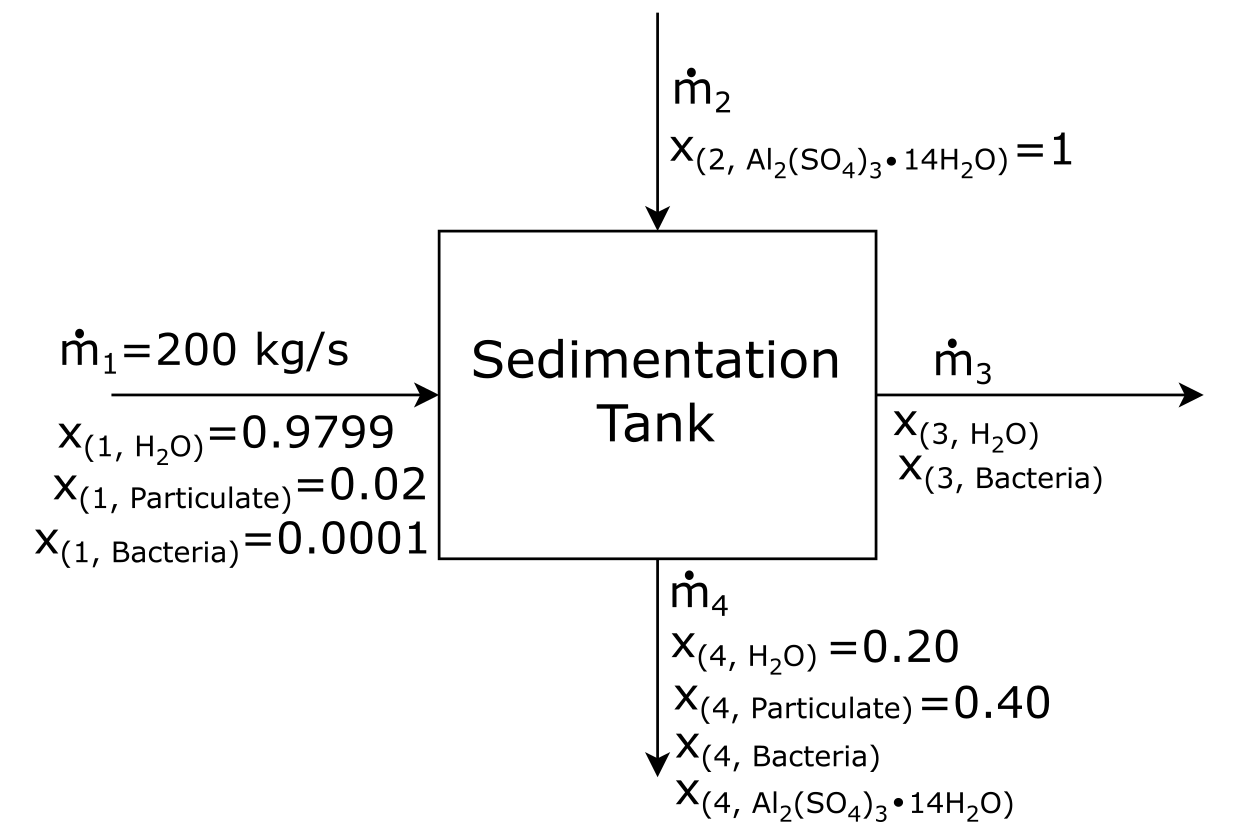
Attribution: Said Zaid-Alkailani & UBC [CC BY 4.0 de (https://creativecommons.org/licenses/by/4.0/)]
b) Perform a degree of freedom analysis¶
We have 7 unknowns, so we need to find 7 equations. First lets do all of the mass balances:
Now lets do the mass fraction balance:
Next lets write our the extra equation:
Finally we can solve for the degrees of freedom:
c) Fully balance the remainder of the block flow diagram¶
To fully we balance the diagram we must first solve for all of the unknowns.
1. Solve for \(\dot{m}_4\) using particulate balance:¶
2. Solve for \(x_{(4, Bacteria)}\) using the extra equation:¶
3. Solve for \(x_{(4, \space Al_2 (SO_4)_3 \cdot 14 H_2 O)}\) using the fractional mass balance:¶
4. Solve for \(\dot{m}_2\) using the alum balance:¶
5. Solve for \(\dot{m}_3\) using a combination of the water balance and bacteria balance:¶
We can equate these two equations to get:
and using the fractional mass balance
we can solve for \(x_{(3, \space Bacteria)}\)
Now that we have completely solved the material balance, we can complete our BFD:

Attribution: Said Zaid-Alkailani & UBC [CC BY 4.0 de (https://creativecommons.org/licenses/by/4.0/)]
In [ ]: